IL PARADOSSO DI ACHILLE E LA TARTARUGA YouTube

Achille e la Tartaruga l’Europa a due velocità Vector WM

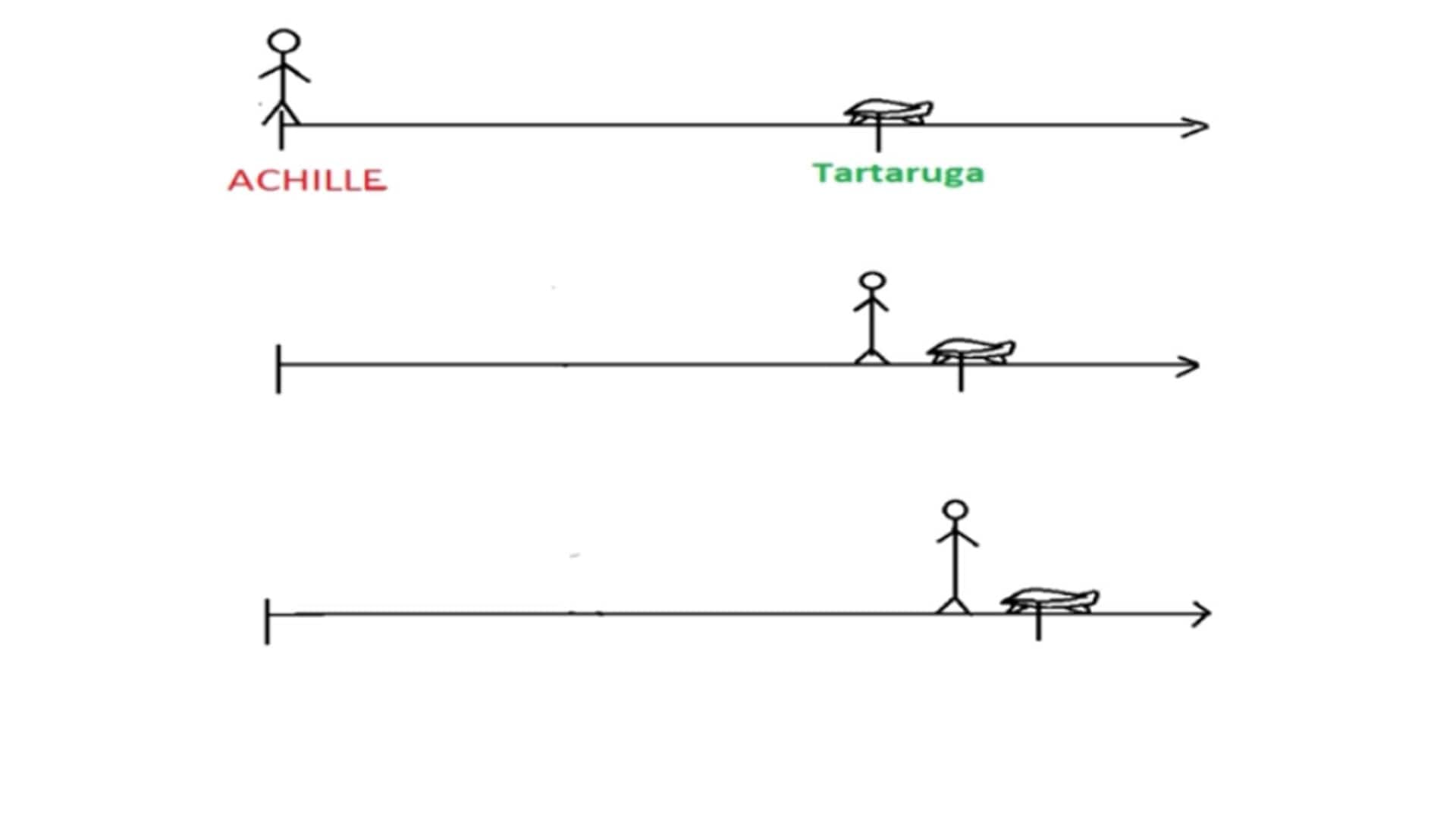
Il paradosso era fondato su questo presupposto: nel tempo che Achille impiega per raggiungere il punto in cui inizialmente si trova la tartaruga (A1, vedere disegno), quest'ultima avrà, comunque, percorso un piccolo tratto (T0-T1). Quando Achille avrà percorso questo piccolo tratto (A1-A2), la tartaruga sarà ulteriormente avanzata (T1-T2).

Achille e la tartaruga il paradosso di Zenone YouTube

Sicuramente avrete sentito parlare del paradosso in cui l'eroe greco Achille viene battuto sul tempo da una tartaruga. Spieghiamo perché Zenone lo sosteneva e come si si supera facilmente. A cura di Camilla Ferrario. 3.642 condivisioni. Uno dei paradossi logici più famosi di sempre è stato realizzato dal filosofo dell'antica Grecia Zenone.

Zenone e il Paradosso di Achille e la Tartaruga YouTube

Formulazione del paradosso di Achille e la tartaruga. Il piè veloce Achille e una tartaruga si sfidano in una gara di corsa. Se alla tartaruga viene dato un vantaggio iniziale, allora Achille non riuscirà mai a raggiungere la tartaruga. Uno dei motivi per cui si ha difficoltà nel comprendere tale paradosso è che si presta poca attenzione al.

Achille e la tartaruga, la spiegazione semplice del paradosso di Zenone

Il paradosso di Achille e la tartaruga risale al V secolo a.C. Fu proposto da Zenone di Elea ed è diventato, nel corso del tempo, il paradosso più noto esposto dal filosofo. Prima di procedere a illustrare il paradosso di Achille e tentare di spiegarlo, è utile dare una definizione di cosa esso sia tecnicamente, così come è importante lasciare qualche informazione sul suo ideatore.

Il paradosso di Achille e la tartaruga di Zenone di Elea Matematica e Filosofia YouTube

Paradosso di Achille e la tartaruga: risoluzione 'matematica' I paradossi della matematica. Paradosso di Achille e la tartaruga. Risoluzione matematica del paradosso con riferimenti alle serie numeriche convergenti. Materia: Matematica e Fisica. Destinatari: studenti del terzo anno dei licei non scientifici.

Perché Achille raggiungerà la tartaruga? Bar Scienza

La corsa della tartaruga La descrizione di Aristotele. Aristotele espone il paradosso così (Fisica, Libro VI, capitolo 9, 239b 14-20) : «Il secondo argomento prende il nome "dell'Achille" e consiste in questo: nel momento in cui il concorrente più veloce parte dopo il concorrente più lento nella corsa, quest'ultimo non sarà mai raggiunto dal più veloce perché l'inseguitore prima sarebbe.

Il paradosso di Achille e la tartaruga, di Zenone di Elea Meer

Da un paradosso all'altro Il fascino di questa gara impossibile ha travalicato i limiti della filosofia. Lewis Carroll, l'autore di Alice nel paese delle meraviglie e scrittore molto amato dai filosofi per i suo racconti intrisi di logica, immagina che a corsa finita Achille abbia finalmente raggiunto la tartaruga, ma questa lo sottoponga a un nuovo dilemma, che riguarda non più il movimento.

Zenone e il Paradosso di Achille e la Tartaruga YouTube

Risoluzione matematica del paradosso con riferimenti alle serie numeriche convergenti. Materia: Matematica e Fisica. Destinatari: studenti del terzo anno dei licei non scientifici. Professoressa: Patrizia Valle. Matematica. lezioni. La scuola in tivu. Paradosso di Achille e la tartaruga: risoluzione 'matematica' - I paradossi della matematica.

Cos’è il paradosso di Achille e la tartaruga? Focus.it

Una delle descrizioni più famose del paradosso è dello scrittore argentino Jorge Luis Borges: «Achille, simbolo di rapidità, deve raggiungere la tartaruga, simbolo di lentezza. Achille corre dieci volte più svelto della tartaruga e le concede dieci metri di vantaggio. Achille corre quei dieci metri e la tartaruga percorre un metro; Achille.

Interesting Paradoxes and Puzzles HubPages

Il paradosso di Zenone. Se Achille facesse una gara con una tartaruga facendola partire con un piede di vantaggio, l'eroe non riuscirebbe mai a raggiungerla. Questo perché Achille dovrebbe prima coprire il piede di vantaggio, ma nel frattempo la tartaruga sarà avanzata di un po'. E così all'infinito.

Achilles und die Schildkröte Alberigo Albano Tuccillo

Riuscirà Achille a raggiungere la lenta Tartaruga?Il paradosso di Achille e la TartarugaNota Matematica:S è una serie geometrica q^n con q=1/2 e q € (-1,1) e.

Paradosso di Achille e la tartaruga risoluzione ' fisica ' Rai Cultura

Il paradosso di Zenone di Achille e la Tartaruga è nato nel Cilento, nell'attuale Velia.Ad elaborare il paradosso è stato Zenone di Elea, allievo di Parmenide e della Scuola eleatica fondata da Parmenide stesso. Parmenide, la Scuola eleatica e quindi Zenone sono figli della Magna Grecia, precisamente di Elea, l'attuale Velia che troviamo nel comune di Ascea.

Achille e la tartaruga, la spiegazione semplice del paradosso di Zenone

Nel paradosso è supposta l'esistenza di una costante d tale che v T v A = d, ad esempio d = 1 / 10 se Achille va 10 volte più veloce della tartaruga. La legge del moto rettilineo uniforme afferma che x A ( t) = s 0 + v A t = v A t visto che fissiamo la posizione iniziale di Achille a 0. Per la tartaruga vale invece x T ( t) = L 0 + v T t.

Paradossi di Zenone di Elea descrizione, significato e fatti interessanti

Achille e la tartaruga: il paradosso di ZenoneAchille e la tartaruga: percorso di approfondimento sul paradosso di Zenone. Spiegazione e la soluzione matemat.

Il paradosso di Achille e la tartaruga spiegato da Zanc9 Problemi per tutti 1 YouTube

Il paradosso di Achille e la Tartaruga del filosofo Zenone di Elea ci è giunto nella descrizione fattane da Aristotele (384-322 a.C.) nella Fisica. Riportiamo qui di seguito una sua possibile.

Paradosso Di Achille E La Tartaruga garurris

- Paradosso di Achille e della Tartaruga. Achille, Il corridore più rapido del mondo non raggiungerà mai la tartaruga, se questa ha un, sia pur piccolo, vantaggio. Achille infatti dovrà prima di tutto raggiungere il punto in cui si trovava la tartaruga al momento del via. Mentre Achille percorre questo tratto la tartaruga si sarà spostata.