
quando una funzione è continua in un intervallo chiuso Lettera43
Continuita di funzioni. Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva. Universita degli Studi di Padova Dipartimento di Matematica. 2 novembre 2015. De nizione (Continua in c) Sia I un intervallo aperto, c 2 I e f : I ! R. La funzione f e. continua in c se esiste lim f (x) x!c. e vale f (c). De nizione (Continua in I aperto)

Continuità di una funzione Andrea il Matematico
Una funzione f (x) si dice continua in un intervallo I se essa è continua in ogni punto di I. L'insieme dei valori di x per cui una funzione è continua è detto insieme di continuità di f (x).

Limite di una funzione definizione e sua verifica tramite la definizione . YouTube
Funzione continua in un intervallo. Una funzione f (x) si dice continua nell'intervallo [A,B] se è continua in ogni punto dell'intervallo (A,B) e sugli estremi si ha limite di f (x) per x.

Funzioni crescenti e decrescenti Altramatica
Teorema sulle funzioni invertibili su un intervallo. Teorema dell'inversa continua. Esempi di funzioni continue invertibili su intervalli. (Versione 01/10/2020) Intervalli di R. De nizione (Segmento) Dati x; y 2 R, x y, il segmento compatto (chiuso e limitato) determinato da x e y, denotato [x; y], e l'insieme: [x; y] = ft 2 R j x t yg.

Intervalli numerici Matematica Dolce
Una funzione si definisce continua in un punto quando disegnandola non stacchiamo mai la biro dal foglio. Proviamo ad osservare il grafico della retta. Si tratta di una retta inclinata a 45 gradi, crescente, e con intercetta all'origine pari a 1.

Teoremi TEOREMA DI ROLLE Data una funzione definita in un intervallo chiuso tale che sia
L'unica condizione necessaria è che la funzione sia continua nell'intervallo considerato. Ad esempio, nel grafico precedente la funzione è uniformemente continua in [b,c] con la relazione δ=2ε. Nell'intervallo [a,b] è uniformemente continua con la relazione δ=ε. Infine, nell'intervallo [0,a] è soltanto continua rispetto alla relazione δ=ε/2.

Intervalli Definizioni ed Esempi YouTube
Tags: metodo per controllare se una funzione è continua in un punto - verifica della continuità in un punto. Ultima modifica: 19/04/2023. Definizione di funzione continua in un punto e metodo per stabilire se una funzione è continua in un punto, con esempi ed esercizi svolti.
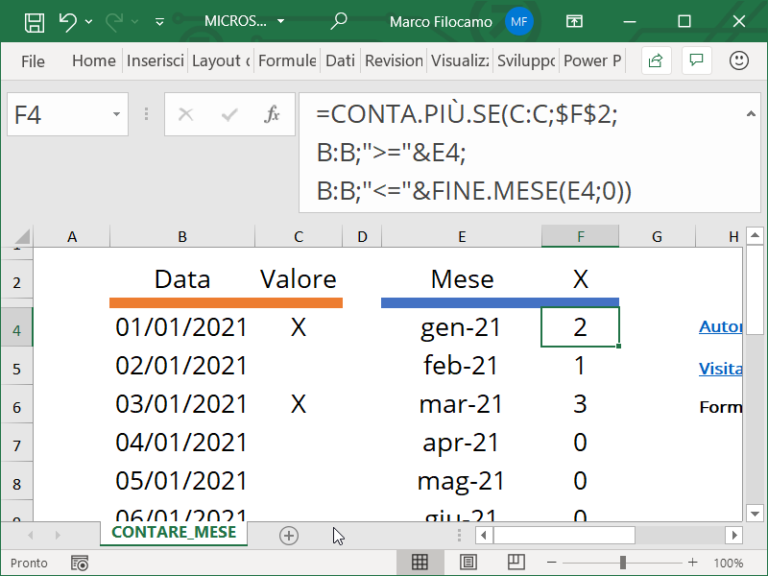
Scopri come contare le celle in un intervallo date con Excel
Esempi di funzione continue. La funzione costante y = k y = k è continua in R R. La funzione identica y = x y = x è continua in R R. Ogni funzione polinomiale è continua in R R. Ogni funzione razionale fratta y = p(x) q(x) y = p ( x) q ( x) è continua in R −x, q(x) = 0 R − x, q ( x) = 0. Le funzioni y = cosx y = cos. x e y = sinx y = sin.

Lezione di Analisi Definizione di continuità di una funzione in un punto YouTube
Tags: esercizi sulle funzioni continue e sulla continuità in un punto o su un intervallo, definite a tratti e non, con soluzioni e spiegazioni su come risolverli. Ultima modifica: 28/09/2023

grafico di una funzione continua GeoGebra
Sia I ⊂ R un intervallo e sia f(x) una funzione continua in I. Se f(x) assume due valori distinti y_1 < y_2 in I, allora f(x) assume tutti i valori compresi tra y_1 e y_2. In termini un po' più tecnici: ∀ y_0 : y_1 ≤ y_0 ≤ y_2 ∃ x_0∈ I tale che f(x_0) = y_0. Dimostrazione del teorema dei valori intermedi

Segno e zeri funzione (grafico) YouTube
Funzioni continue su un intervallo. Proprietà puntuali o globali. Nello studio delle proprietà delle funzioni continue, lo studente ha incontrato teoremi di tipi diversi. Confrontiamo tra loro questi due enunciati: Teorema 1 Siano f; g : [a; b] ! R funzioni continue in [a; b]. Allora anche. f + g è continua in [a; b] :

Funzioni continue
Funzione continua. La funzione di cui sopra è continua perché può essere disegnata in un colpo solo senza staccare la mano dal foglio. D'altra parte, quando la precedente condizione di continuità non è inserita in una funzione, si dice che sia una funzione discontinua . Funzione discontinua.

TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE Andrea il Matematico
Risulta. f(c) = 0 L'ascissa c rende 0 la funzione e prende anche il nome di 'zero della funzione f(x)'. Due caratteristiche essenziali di f(x): l'arco AB non ha interruzioni, cioè la funzione è continua nell'intervallo [2, 4]; i punti A e B sono da parti opposte rispetto all'asse x, cioè f(2) e f(4) hanno segno opposto.

Esercizi svolti sulle funzioni pari e dispari 1 Esame di Matematica Generale YouTube
La continuità di una funzione in un punto o su un intervallo fornisce intuizioni fondamentali sul suo comportamento. Una funzione continua non presenta salti, discontinuità o asintoti nel suo grafico; il che significa che può essere disegnata senza sollevare la penna dal foglio. Questa proprietà è fondamentale per molteplici ragioni:

Definizione di continuità di una funzione, in un punto e in un intervallo YouTube
Una funzione si dice continua in un intervallo quando è continua in ogni punto dell'intervallo. Definizione. Una funzione si dice continua se é continua in ogni punto del dominio.
Funzione continua in un intervallo
Teorema di integrabilità delle funzioni continue. Se una funzione f (x) è una funzione continua nell'intervallo [a,b] allora la funzione è integrabile secondo Riemann in [a,b] Dimostrazione. In base al teorema di Cantor una funzione limitata in un intervallo chiuso [a,b] è uniformemente continua. Quindi è anche continua.