6° lezione gli assiomi YouTube

Calaméo Assiomi della comunicazione

è valida. Questo assioma stabilisce semplicemente che se sappiamo che () per qualche proprietà e è un particolare termine nel linguaggio (cioè rappresenta un particolare oggetto nella struttura che stiamo trattando), allora dovremo essere in grado di affermare ().. Un esempio simile è: Assioma di generalizzazione esistenziale. Data una formula in un linguaggio del primo ordine , una.

Che cos'è l' inquinamento luminoso YouTube

Un assioma, in epistemologia, è una proposizione o un principio che è assunto come vero perché ritenuto evidente o perché fornisce il punto di partenza di un quadro teorico di riferimento.. L'insieme degli assiomi e dei concetti primitivi costituiscono il fondamento, il "punto di partenza", o l'inizio, di ogni teoria deduttiva che si presenti come sistema assiomatico (v.

Appunti di matematica Assiomi euclidei YouTube

Assioma. In epistemologia, un assioma è una proposizione o un principio che viene assunto come vero perché ritenuto evidente o perché fornisce il punto di partenza di un quadro teorico di riferimento. L'insieme degli assiomi e dei concetti primitivi costituiscono il fondamento, il "punto di partenza", o l'inizio, di ogni teoria deduttiva che.

Gli enti fondamentali e i primi assiomi della geometria YouTube

assioma proposizione che si assume come vera e a partire dalla quale, tramite una catena di deduzioni, si dimostrano altre proposizioni dette teoremi.Mentre fino al xviii secolo gli assiomi erano considerati verità matematiche evidenti per sé stesse, che si accettavano senza dimostrazione, in seguito allo sviluppo delle geometrie non euclidee il requisito dell'evidenza è stato lasciato.

Assioma YouTube

L'assioma di completezza assicura quindi l'esistenza di almeno un numero reale c che si interpone tra gli elementi dell'insieme A e gli elementi dell'insieme B. In questo caso gli elementi separatori sono infiniti, infatti ogni numero reale c appartenente all' intervallo [0,1] soddisfa la doppia disuaglianza a ≤ c ≤ b.

Che cos'è un bambino?

Un assioma è una proposizione matematica che si considera vera senza essere dimostrata; gli assiomi sono il fondamento di qualsiasi teoria e devono essere tra loro indipendenti, non contradditori e in numero finito.. Quando si dimostra un teorema si fa riferimento ad altri teoremi, lemmi o corollari precedentemente dimostrati, che a loro volta dipendono da altri.

COSA SIGNIFICA AVERE UNA STOMIA docvadis.it · stomia non è un malato cronico, questo è l

Un assioma è una proposizione o una regola che viene considerata come vera senza bisogno di dimostrazione. Gli assiomi costituiscono le basi di un sistema formale o di una teoria matematica, e a partire da essi si possono derivare tutte le altre proposizioni o regole all'interno del sistema.

PPT I primi elementi della geometria PowerPoint Presentation, free download ID4971077

Questo assioma indica che è possibile tracciare un cerchio usando un compasso con un centro prefissato e un raggio prefissato. Assioma della congruenza: "Tutti i segmenti uguali sono congruenti." Questo assioma afferma che se due segmenti hanno la stessa lunghezza, sono congruenti e possono sovrapporsi perfettamente. Assioma della somma.

Assioma

04 Assiomi YouTube

Un assioma in matematica è un enunciato che anche se non può essere dimostrato, è considerato vero. Un esempio di assioma matematico è il postulato "Due rette parallele non si incontrano mai".. non esisteva una vera analogia tra il nome della cosa e quello che rappresenta. Per esempio se pensiamo alla parola casa, la sequenza delle.

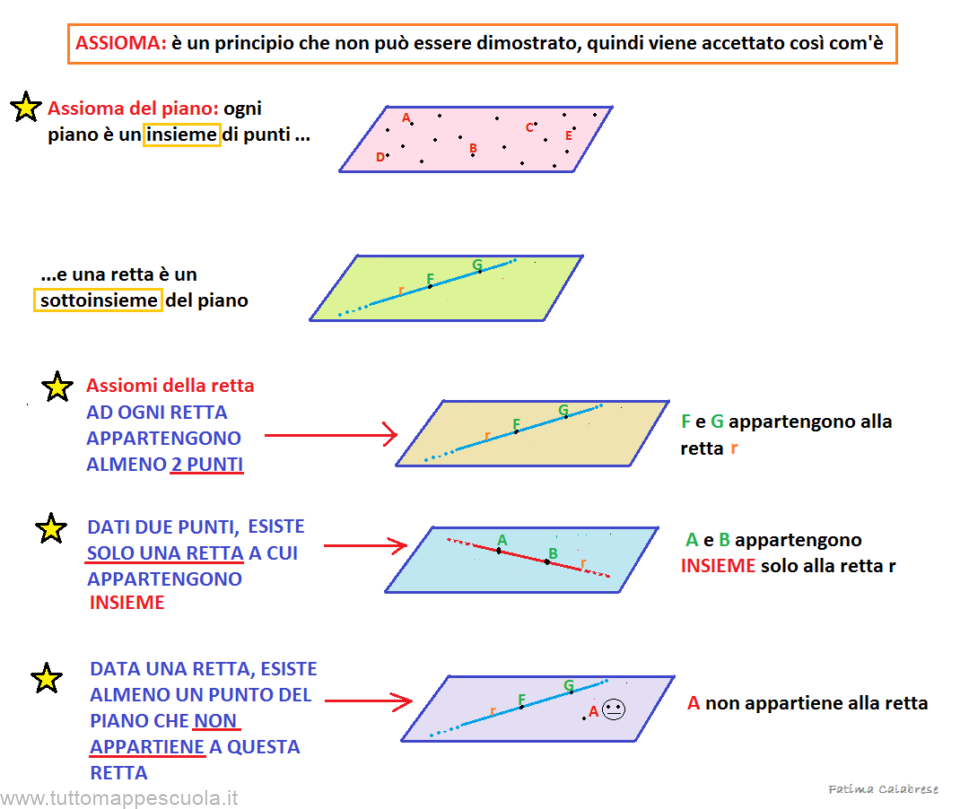
Assioma del piano e della retta Tutto Mappe Scuola

assioma. assiòma s. m. [dal lat. tardo axioma - ătis, gr. ἀξίωμα -ατος der. di ἄξιος «degno»] (pl. - i ). - Nel linguaggio com., verità o principio che si ammette senza discussione, evidente di per sé. In filosofia, principio certo per immediata evidenza e costituente la base per l'ulteriore ricerca; in partic., nella.

Differenza di insiemi. Insieme complementare. Matematica terza media

La differenza tra postulati e assiomi. In origine, nella filosofia greca, i termini "postulato" e "assioma" avevano significati leggermente diversi: Un postulato era una proposizione che veniva accettata come vera senza prova o dimostrazione, perché serviva come punto di partenza per un ragionamento o un'argomentazione.

L'ausiliare nei tempi composti Imparare l'italiano, Grammatica, Lezioni di grammatica

Quando un teorema è stato dimostrato, si dice che I è condizione sufficiente per il verificarsi di T e che T è condizione necessaria per il verificarsi di I.. - cos'è un assioma; - cos'è un corollario; - cos'è un lemma. Autore: Giuseppe Carichino (Galois) Ultima modifica: 20/10/2023. Contattaci; Staff e Collaboratori;

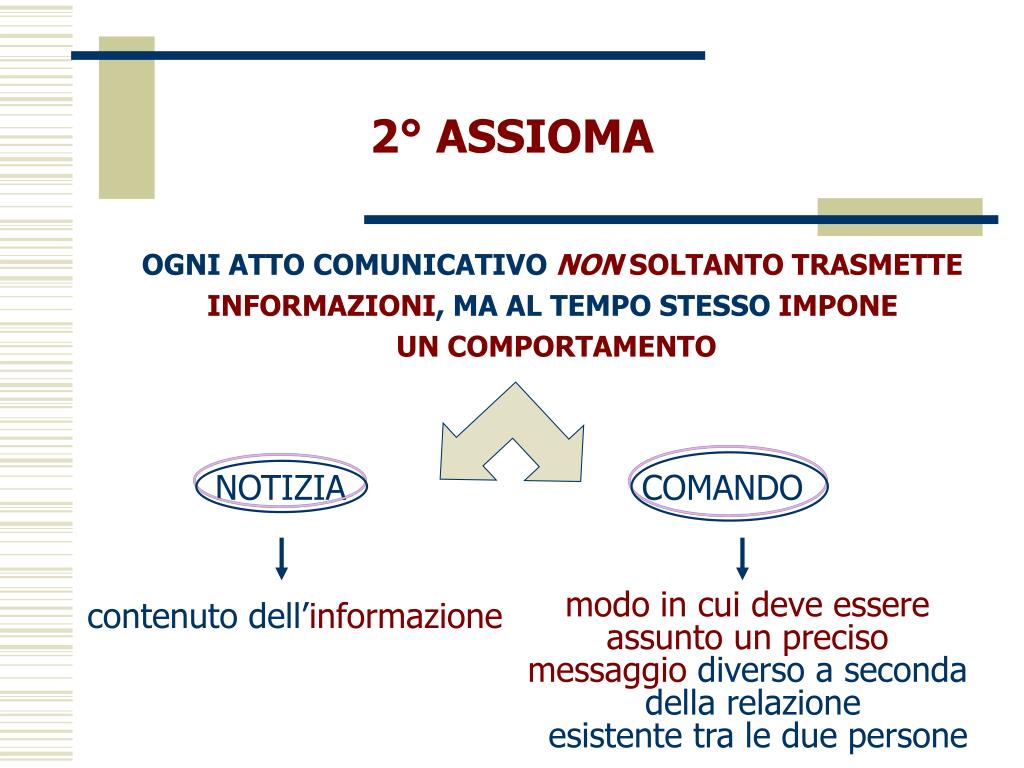
PPT LA COMUNICAZIONE PowerPoint Presentation, free download ID192236

Che cosa è un assioma? Ultimo aggiornamento: 11 ottobre 2023. Un assioma è una proposizione o una regola che viene considerata come vera senza bisogno di dimostrazione. Gli assiomi costituiscono le basi di un sistema formale o di una teoria matematica, e a partire da essi si possono derivare tutte le altre proposizioni o regole all'interno.

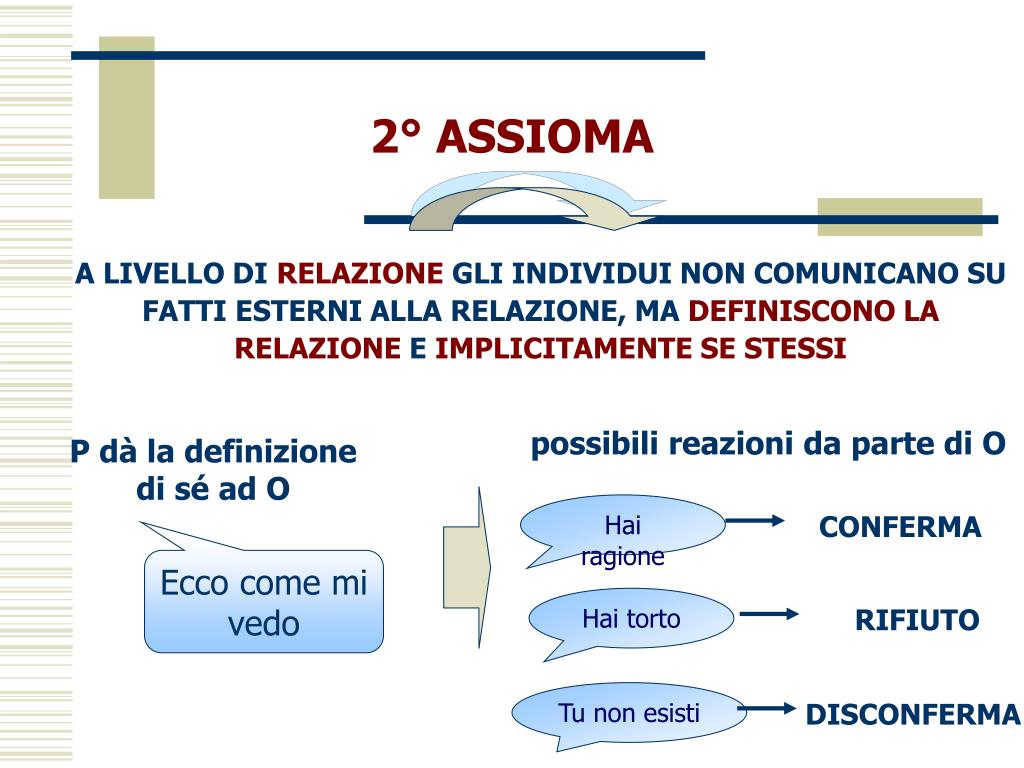
PPT LA COMUNICAZIONE PowerPoint Presentation, free download ID192236

Un assioma è una proposizione fondamentale e indimostrabile di un sistema logico o di una teoria matematica. Le caratteristiche che definiscono un assioma sono: 1. Indipendenza: Gli assiomi sono considerati indipendenti, cioè non possono essere derivati da altri assiomi o teoremi all'interno del sistema. 2.

cos'è un meme e come si pronuncia YouTube

L' assioma del trasporto di un segmento, noto anche come postulato del trasporto dei segmenti, è un principio geometrico fondamentale che afferma: Data una semiretta di origine O e un segmento AB, esiste un unico punto P tale che i segmenti AB e OP siano congruenti tra loro AB ≌ OP A B ≌ O P. In pratica, è sempre possibile trasportare un.